Table of Contents
In 2018, this post made an interesting attempt at solving Bongard problems using deep learning. That work may have laid the foundation for further attempts at creating various Bongard-like datasets such as Bongard-LOGO1, Bongard-HOI2, and Bongard-OpenWorld3. This post is an attempt to replicate the same methodology with state-of-the-art vision-language models (VLMs).
A Quick Intro
Bongard Problems are puzzles formulated by Russian scientist and intelligence theorist Mikhail Moiseevich Bongard in the 1960s in his book The Problem of Recognition (Problema Uznavaniya). A typical Bongard problem consists of two sets of six images. All images on one side illustrate a shared concept that is absent from the other side.
The task for the user is to discover the distinguishing concept and express it in natural language.
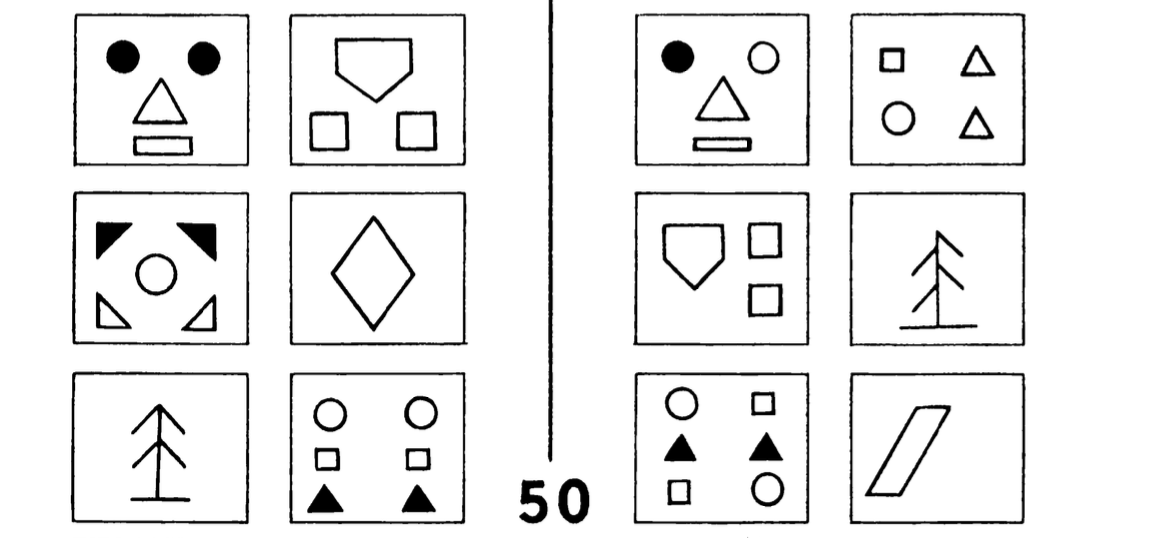
Originally there were only 100 puzzles in the book. Later, Douglas Hofstadter popularized them through his Pulitzer Prize-winning book Gödel, Escher, Bach 4 and added a few more. His doctoral student Harry Foundalis added even more Bongard problems and developed an interesting system, Phaeaco, that turned visual patterns into concepts. Harry still maintains a page for Bongard problems and accepts new submissions 5.
Bongard problems are particularly challenging for AI systems because of their demand for abstract pattern recognition from minimal examples. Unlike typical classification benchmarks where models are trained on thousands of labeled examples, Bongard problems require extracting underlying concepts from just a few examples per group. Here a model must learn from these few examples, infer a rule that distinguishes the two groups, and then correctly classify a novel query image.
Methodology
It's 2025, and VLMs have come a long way from generating captions for images to serving as general-purpose multimodal reasoning agents that can analyze complex visual scenes, solve mathematical problems from diagrams, generate and edit code from screenshots, engage in sophisticated visual conversations, and even control computer interfaces through visual understanding.
In his post, Sergii used CNNs (Convolutional Neural Networks), pre-trained on a dataset of one million randomly generated shapes, and then applied them to Bongard problems. They chose classification over generating natural language explanations of the rules, since that was the best those models could do at the time.
That work predated the modern era of vision-language models such as CLIP (2021), BLIP (2022), and GPT-4V (2023).
Dataset Preparation
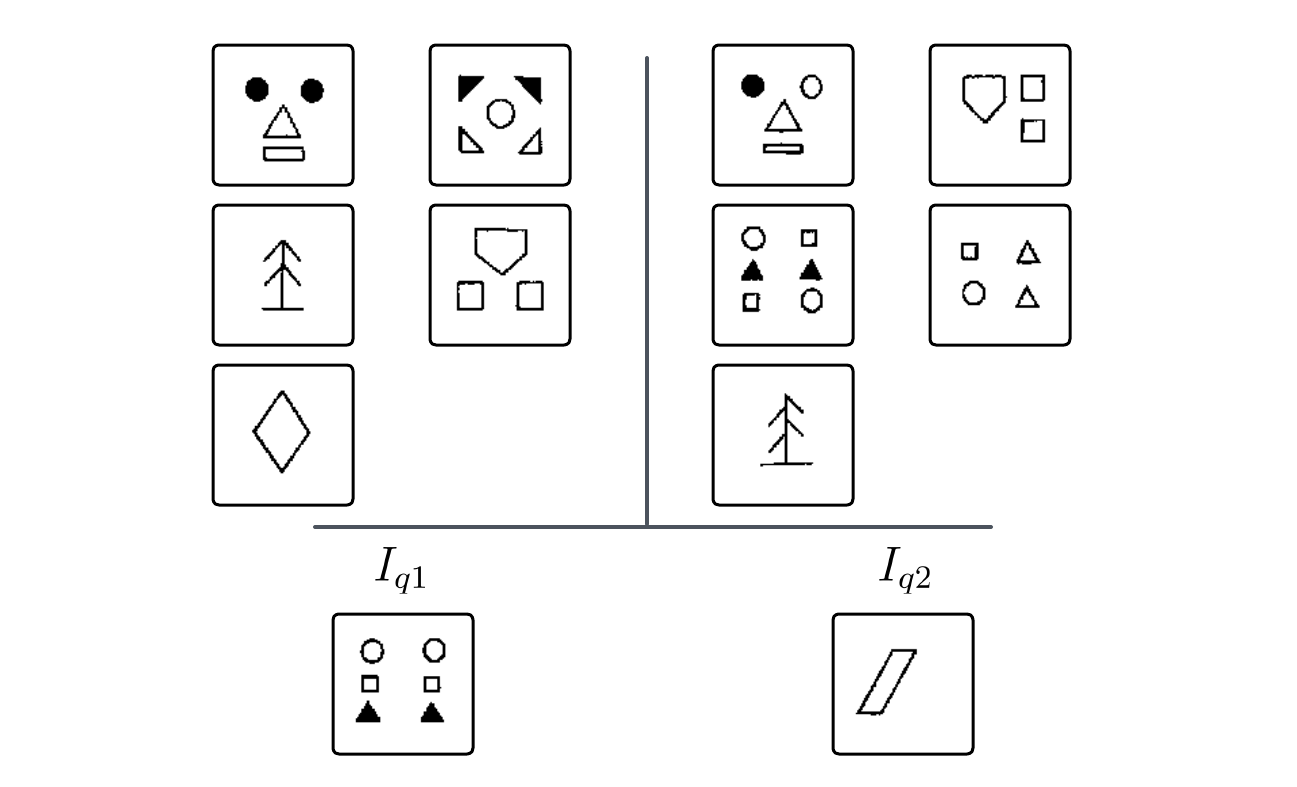
For this experiment, I used Sergii's dataset based on the Bongard problems. The problems are digitized, and each image is split into 12 pieces, each containing a single figure. The first five figures on each side serve as examples for the models, while the sixth figure is used as a query image. Each problem is divided into two sets, with one query image taken from each side.
Sergii's dataset missed the 77th problem, I have added it to mine and can be found here.
In total, I used 232 problems, resulting in 464 queries.
Vision Language Models
For this experiment I have used these following models:
- GPT-5
- Gemini 2.5 Flash
- Gemini 2.0 Flash
- Qwen V2.5L - 72B
OpenAI and Google models were accessed via their respective APIs, while Qwen V2.5L was accessed through the Ollama interface.
Implementation
Vision models are provided with five images from group A, five images from group B, and a query image, all at once. The task is to classify the query image as belonging to either group A or group B.
The models are asked to produce a structured JSON output with the following fields.
{
"left_rule": "The rule that defines group_a (e.g., 'Spiral curls counterclockwise')",
"right_rule": "The rule that defines group_b (e.g., 'Spiral curls clockwise')",
"query_image": "What you observe in the query image regarding the rule",
"analysis": "Describe what made you make this decision",
"confidence": "0 to 100",
"classification": "group_a or group_b"
}Results & Analysis
The results show substantial improvement over Sergii's 2018 CNN
approach. GPT-5 unsurprisingly performed the best with 73.2%
accuracy with correctly classifying 340 problems out of 464.
| Model | Total | Correct | Wrong | Accuracy |
|---|---|---|---|---|
| GPT-5 | 464.0 | 340.0 | 124.0 | 73.275862 |
| Gemini 2.5 Flash | 464.0 | 311.0 | 153.0 | 67.025862 |
| Gemini 2.0 Flash | 464.0 | 275.0 | 189.0 | 59.267241 |
| Qwen V2.5L 72B | 464.0 | 270.0 | 194.0 | 58.189655 |
Looking at full Bongard problems (232 total), we can distinguish between completely solved (both variants correct), partially solved (only one variant correct), and completely unsolved problems.
| Model | Accuracy | Fully Solved | Partially Solved | Unsolved |
|---|---|---|---|---|
| GPT-5 | 89.7% | 132 (56.9%) | 76 (32.8%) | 24 (10.3%) |
| Gemini 2.5 | 86.2% | 111 (47.8%) | 89 (38.4%) | 32 (13.8%) |
| Gemini 2.0 | 81.5% | 86 (37.1%) | 103 (44.4%) | 43 (18.5%) |
| Qwen V2.5L 72B | 82.8% | 78 (33.6%) | 114 (49.1%) | 40 (17.2%) |
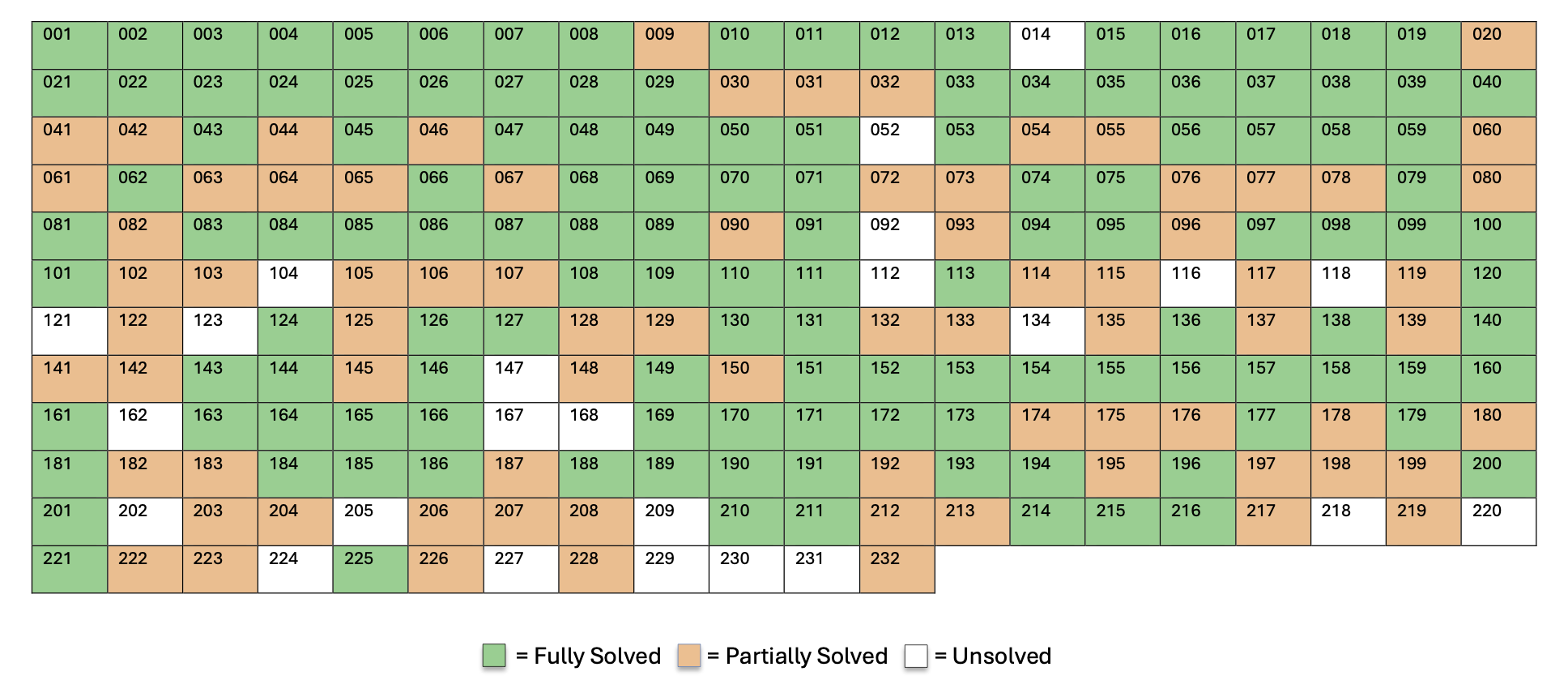
The grid visualization above shows GPT-5's performance across all 232 Bongard problems, with each numbered cell representing one problem. Green cells indicate problems where both variants (a and b) were solved correctly, orange cells show partial solutions (only one variant correct), and white cells represent completely unsolved problems.
Among the models tested, only GPT-5 provided realistic confidence scores in the format analyzed. GPT-5 exhibited a moderate positive correlation between confidence and accuracy (r=0.401, p<0.001). This suggests that when GPT-5 reports higher confidence in its classifications, it is indeed more likely to be correct, though the relationship is not perfect. The model might have some meaningful self-awareness of its performance quality.
Conclusion
This is one of the most straightforward approaches to solving Bongard problems using VLMs. The implementation is simple and basically mimics how a human would approach it; just paste the images in the chat prompt and hope for the best.
As part of this experiment, I also collected the rule in natural language that distinguishes the left set from the right, just as Bongard intended. However, I didn't have enough time to actually evaluate those rules or turn this blog post into an Arxiv preprint.
The code for this experiment can be found here for further inspection: mrprofessor/bongard_vlm
Footnotes
Bongard-LOGO: A New Benchmark for Human-Level Concept Learning and Reasoning.
Bongard-HOI: Benchmarking Few-Shot Visual Reasoning for Human-Object Interactions.
Bongard-OpenWorld: Few-Shot Reasoning for Free-form Visual Concepts in the Real World.